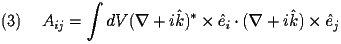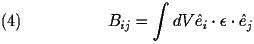Finite Element Discretization
Writing the electric field as
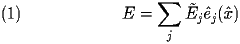
The finite elements
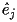 vary linearly in the directions orthogonal
to
vary linearly in the directions orthogonal
to
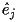 . For example, edges pointing in the x-direction vary linearly in the
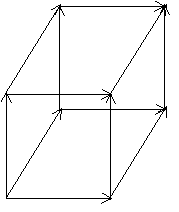
y and z directions but the value of the field remains constant along x. Below is a diagram of an element with the edge vectors shown.
. For example, edges pointing in the x-direction vary linearly in the
y and z directions but the value of the field remains constant along x. Below is a diagram of an element with the edge vectors shown.
A standard finite element discretization technique [see reference] is applied to the vector Helmholtz equation. Using expansion (1)
we get
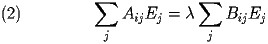
where
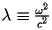 ,
,
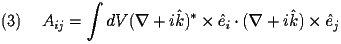
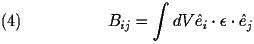
Both of these matrices (A and B) are sparse and the integrations are done over the unit cell. Also, recall that we could as easily replaced the E's in the above equations with H's (keeping in mind the different B.C.'s)
Ryan McClarren

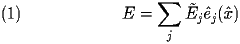
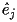 vary linearly in the directions orthogonal
to
vary linearly in the directions orthogonal
to
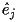 . For example, edges pointing in the x-direction vary linearly in the
y and z directions but the value of the field remains constant along x. Below is a diagram of an element with the edge vectors shown.
. For example, edges pointing in the x-direction vary linearly in the
y and z directions but the value of the field remains constant along x. Below is a diagram of an element with the edge vectors shown.

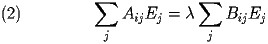
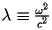 ,
,