Determining H from E (or vice-versa)
Now that we have both
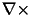 and
and
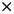 operations defined on our fields
we can go from one to the other (e.g. from E to H) using those operations.
Given the stationary Maxwell Equations previously mentioned
operations defined on our fields
we can go from one to the other (e.g. from E to H) using those operations.
Given the stationary Maxwell Equations previously mentioned

It follows that
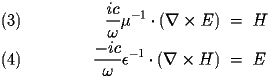
Supposing we had the E field solution to our vector Helmholtz equation. We could determine our H field by computing curl of E and applying some other multiplicative operations on E. However, the derivation of one field from another is complicated by the
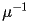 and
and
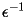 on the left hand side of (3) and (4). These quantities are tensors that can vary from element to element. Fortunately, Curly3d has the ability to track these properties for each element and is able to calculate the required tensor product.
on the left hand side of (3) and (4). These quantities are tensors that can vary from element to element. Fortunately, Curly3d has the ability to track these properties for each element and is able to calculate the required tensor product.
It is also important to point out a relationship that arises in the above equations. By making the following transformation
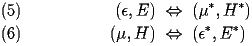
(1) transforms into (2), also conversely (2) becomes (1). Furthermore, the transformation affects (3) and (4) identically.
Curly3d has modules that treat
 's as
's as
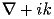 .
.
Poynting Vectors
With the functionality of computing the H field from the E field and vice-versa we can now determine
the Poynting vectors through the unit cell. If we have solved the vector Helmholtz equation for E and we want to
find the Poynting vectors, given

and using (3) we get
![\begin{equation} S \propto E^{*} \times [i \mu^{-1} \cdot ( \nabla \times E)] \end{equation}](EtoH_11.gif)
Using the transformations in (5) and (6) on (8) S can be calculated the same way when we have the H field.
Ryan McClarren
Last modified: Thu Aug 15 14:30:35 EDT 2002
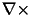 and
and
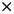 operations defined on our fields
we can go from one to the other (e.g. from E to H) using those operations.
Given the stationary Maxwell Equations previously mentioned
operations defined on our fields
we can go from one to the other (e.g. from E to H) using those operations.
Given the stationary Maxwell Equations previously mentioned 
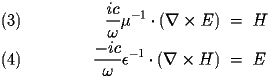
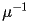 and
and
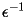 on the left hand side of (3) and (4). These quantities are tensors that can vary from element to element. Fortunately, Curly3d has the ability to track these properties for each element and is able to calculate the required tensor product.
on the left hand side of (3) and (4). These quantities are tensors that can vary from element to element. Fortunately, Curly3d has the ability to track these properties for each element and is able to calculate the required tensor product. 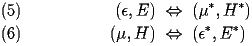
 's as
's as
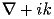 .
.

![\begin{equation} S \propto E^{*} \times [i \mu^{-1} \cdot ( \nabla \times E)] \end{equation}](EtoH_11.gif)