Stationary Maxwell (Wave) Equations
We seek to solve the sationary
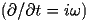 Maxwell equations in the absence of free charges. These equations are:
Maxwell equations in the absence of free charges. These equations are:
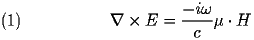
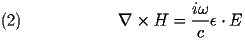
These combine to form two vector Helmholtz equations:

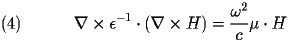
Notice the duality between
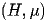 and
and
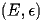 ,both E and H are solutions of a vector Helmholtz equation
we can solve for either by solving the "same" equation. Note however, that E and H satisfy different boundary conditions at the interface of a
perfect conductor; for E the tangential component of the field vanishes at the boundary whereas for H the normal component is zero at the conductor.
,both E and H are solutions of a vector Helmholtz equation
we can solve for either by solving the "same" equation. Note however, that E and H satisfy different boundary conditions at the interface of a
perfect conductor; for E the tangential component of the field vanishes at the boundary whereas for H the normal component is zero at the conductor.
Due to the periodicty of the crystal we seek Bloch wave solutions
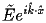 where
where
 is periodic.
Solving for
is periodic.
Solving for
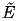 (or
(or
 ) we get
) we get
![\begin{equation} \label{eq:Efinite}
(\nabla + i \hat k) \times [\mu^{-1} \cdot (\nabla + i \hat k) \times \tilde E] = \frac{\omega^{2}}{c^{2}}\epsilon \cdot \tilde E
\end{equation}](MaxEqns_12.gif)
Which we solve in the unit cell volume. This equation is obtained from (3) by replacing
 with
with
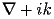 . Henceforth, we shall write
. Henceforth, we shall write
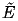 as E for simplicity.
Ryan McClarren
Last modified: Wed Aug 14 13:12:59 EDT 2002
as E for simplicity.
Ryan McClarren
Last modified: Wed Aug 14 13:12:59 EDT 2002
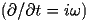 Maxwell equations in the absence of free charges. These equations are:
Maxwell equations in the absence of free charges. These equations are:
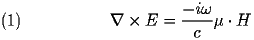
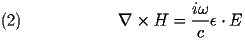

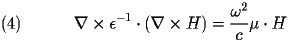
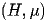 and
and
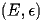 ,both E and H are solutions of a vector Helmholtz equation
we can solve for either by solving the "same" equation. Note however, that E and H satisfy different boundary conditions at the interface of a
perfect conductor; for E the tangential component of the field vanishes at the boundary whereas for H the normal component is zero at the conductor.
,both E and H are solutions of a vector Helmholtz equation
we can solve for either by solving the "same" equation. Note however, that E and H satisfy different boundary conditions at the interface of a
perfect conductor; for E the tangential component of the field vanishes at the boundary whereas for H the normal component is zero at the conductor.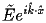 where
where
 is periodic.
Solving for
is periodic.
Solving for
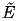 (or
(or
 ) we get
) we get ![\begin{equation} \label{eq:Efinite}
(\nabla + i \hat k) \times [\mu^{-1} \cdot (\nabla + i \hat k) \times \tilde E] = \frac{\omega^{2}}{c^{2}}\epsilon \cdot \tilde E
\end{equation}](MaxEqns_12.gif)
 with
with
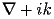 . Henceforth, we shall write
. Henceforth, we shall write
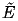 as E for simplicity.
Ryan McClarren
Last modified: Wed Aug 14 13:12:59 EDT 2002
as E for simplicity.
Ryan McClarren
Last modified: Wed Aug 14 13:12:59 EDT 2002