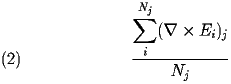Curl of a vector field
After the solution is determined by solving the generalized eigenvalue problem, Curly3d can perform functions on that field. The curl module calculates the curl of the field. The method for performing this calculation is to first take the curl of the field on a face.
For example if we wanted to calculate the curl pointing in the y-direction (into the page positive),
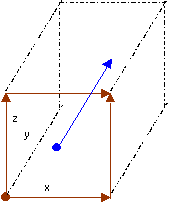
we would first take the line integral of brown field to get the blue field. The line integral gives us the curl on the face by Stokes' theorem:
![\begin{equation} \label{eq:Curlstokes}
\oint d l \cdot F = \int d S[ n \cdot (\nabla \times F)]
\end{equation}](curl_1.gif)
Next, we shift to the opposite face
>
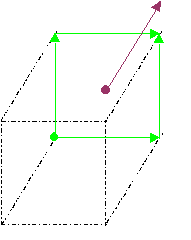
The curl of the green field results in the red field. These vectors are defined on the faces of the cell. Because we desire to have edge defined fields the values of the two curl vectors (blue and red) are averaged and then "exploded" onto the edges in the y direction (orange vectors)
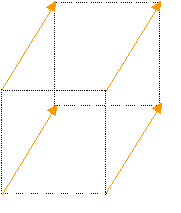
Keeping in mind that
 is actually
is actually
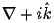 when we take the curl of the field
when we take the curl of the field
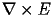 we actually need to calculating
we actually need to calculating
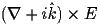 . The cross product module of Curly3d allows for this.
Beyond this there is the issue that an edge can be shared by up to four elements. To correctly represent this for a given edge j
. The cross product module of Curly3d allows for this.
Beyond this there is the issue that an edge can be shared by up to four elements. To correctly represent this for a given edge j
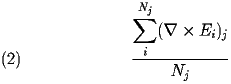
Where N is the number of cells sharing the edge. The implemented computation works correctly for any number (1-4) of cells sharing the edge.
Ryan McClarren
Last modified: Thu Aug 15 09:45:02 EDT 2002


![\begin{equation} \label{eq:Curlstokes}
\oint d l \cdot F = \int d S[ n \cdot (\nabla \times F)]
\end{equation}](curl_1.gif)


 is actually
is actually
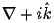 when we take the curl of the field
when we take the curl of the field
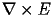 we actually need to calculating
we actually need to calculating
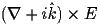 . The cross product module of Curly3d allows for this.
Beyond this there is the issue that an edge can be shared by up to four elements. To correctly represent this for a given edge j
. The cross product module of Curly3d allows for this.
Beyond this there is the issue that an edge can be shared by up to four elements. To correctly represent this for a given edge j